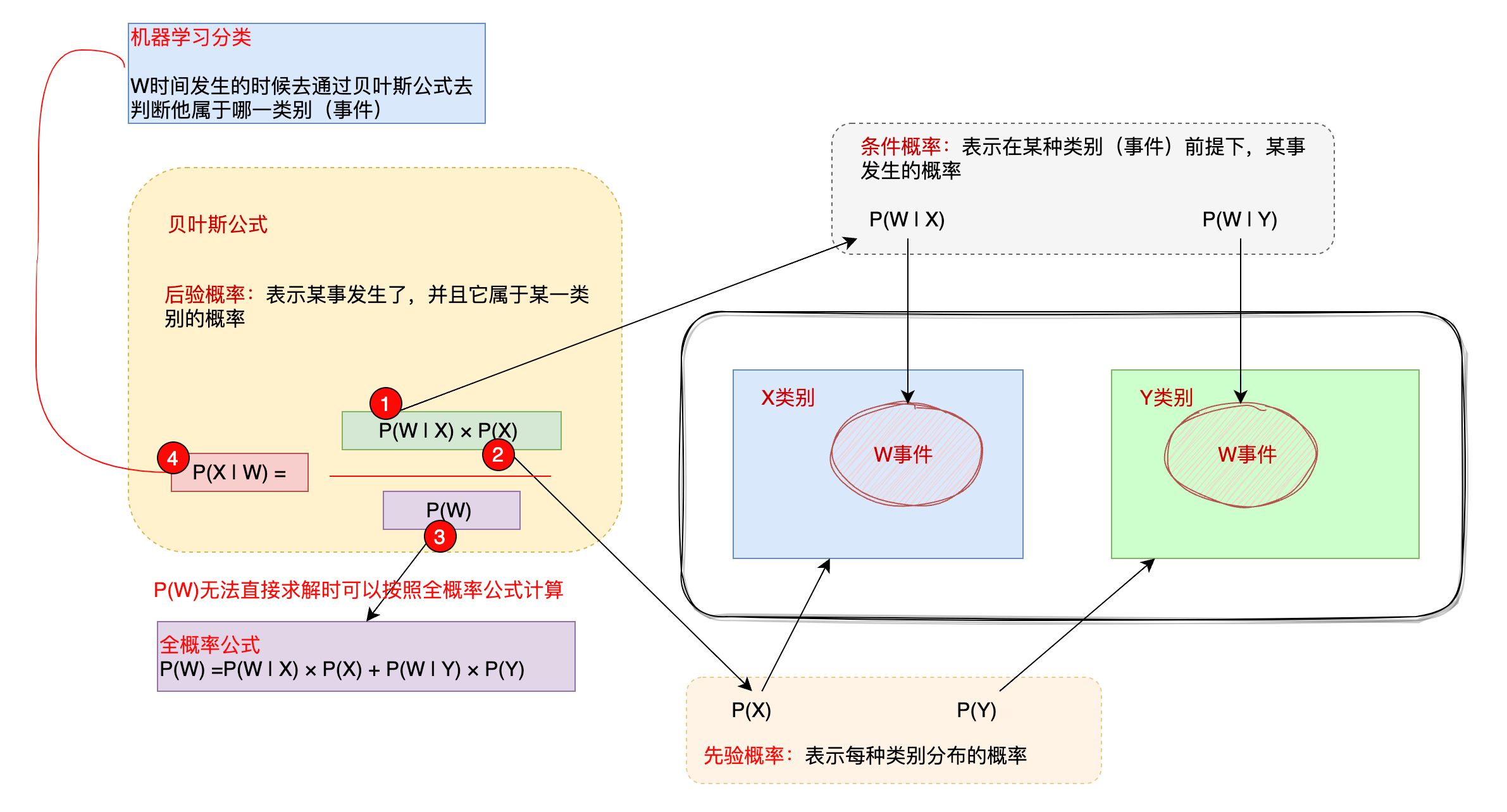
1 一张图解释贝叶斯公式
英国数学家托马斯:贝叶斯( Thomas Bayes),在1763年发表的一篇论文中,首先提出了这个定理
贝叶斯在他的文章中是为了解决一个“逆概率”的问题
贝叶斯公式能够在有限的信息下,帮助我们预测出概率
条件概率表示在某种类别(事件)前提下,某事发生的概率
只要在题设条件中有:**”已知事件A发生”** 或“在事件B发生的条件下〞等,均要考虑条件概率,条件概率帮助我们考虑问题时限在正确的可能性(条件)下
先验概率表示每种类别分布的概率
2 三个示例
2.1 示例1
大年三十晚上,爷爷奶奶发红包。爷爷准备的红包是 4 个 50 元的,6 个 100 元的。奶奶准备的红包是 8 个 50 元的,4 个 100 元的。全家人随机抽,你运气很好,拿到一个 100 元的红包。请问这个红包来自爷爷的概率有多少?来自奶奶的概率有多少?
解答
爷爷一共10个红包,奶奶一共12个红包
分类(事件A)爷爷的概率是P(爷爷) = 10个红包/22个红包=5/11
分类(事件B)奶奶的概率是P(奶奶) = 12个红包/22个红包=6/11
分类(事件A)爷爷条件下(或者理解:范围下),抽中100元红包的概率是=6个红包/10个红包=3/5。这里分母10个红包指得是爷爷一共10个红包
分类(事件B)奶奶条件下(或者理解:范围下),抽中100元红包的概率是=4个红包/12个红包=2/6。这里分母12个红包指得是奶奶一共12个红包
注意:这里全概率P(100)是直接可以求的,不需要全概率公式:P(100)=10个100元红包/22个总红包=5/11【有些时候全概率需要使用全概率公式计算】
根据贝叶斯公式,其实就是求发生了一个事件(抽到了1个100元的红包)来自爷爷还是奶奶的概率
即通过先验概率(爷爷和奶奶分类的全概率)、条件概率(爷爷或奶奶类别或者范围下100元红包的条件概率)得出后验概率(他属于哪个类别(爷爷或奶奶)的概率是多少)
P(爷爷 | 100) = P(100 | 爷爷) × P(爷爷)/ P(100) = (3/5) × (5/11) ÷ (5/11) = 3/5
P(奶奶 | 100) = P(100 | 奶奶) × P(奶奶)/ P(100) = (2/6) × (6/11) ÷ (5/11) = 2/5
| 分析内容 | 分类(事件A)爷爷 | 分类(事件B)奶奶 |
|---|---|---|
| P(W) 先验概率 每种类别的概率 | 5/11 | 6/11 |
| 条件概率 在各分类中某事件的概率 | 3/5 | 2/6 |
| 全概率 某种程度上可以理解先分类再分步 | 5/11(全局均是这个值) | 5/11(全局均是这个值) |
| 后验概率,发生某事件条件下属于这个类别的概率 | 3/5 | 2/5 |
2.2 示例2
在夏季,某公园男性穿凉鞋的概率为1/2,女性穿凉鞋的概率为2/3,并且该公园中男女比例通常为2:1
若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
解答
分类(事件A)男性的概率是P(男性) = 2/3
分类(事件B)女性的概率是P(女性) = 1/3
分类(事件A)男性条件下(或者理解:范围下)穿凉鞋的概率,即条件概率P(凉鞋 | 男性)=1/2
分类(事件B)女性条件下(或者理解:范围下)穿凉鞋的概率,即条件概率P(凉鞋 | 女性)=2/3
注意这里与示例1不一样的地方是,对于全概率是没办法直接求出的,因此利用全概率公式
全概率公式
P(凉鞋) = P(男性) × P(凉鞋 | 男性) + P(女性) × P(凉鞋 | 女性) = 2/3 × 1/2 + 1/3 × 2/3= 5/9
P( 男性 | 凉鞋) = P(凉鞋 | 男性) × P(男性)/ P(凉鞋) = (1/2) × (2/3) ÷ (5/9) = 3/5
P( 女性 | 凉鞋) = P(凉鞋 | 女性) × P(女性)/ P(凉鞋) = (2/3) × (1/3) ÷ (5/9) = 2/5
| 分类(事件A)男性 | 分类(事件B)女性 | |
|---|---|---|
| P(W) 先验概率 每种类别的概率 | 2/3 | 1/3 |
| 条件概率 在各分类中某事件的概率 | 1/2 | 2/3 |
| 全概率 某种程度上可以理解先分类再分步 | 5/9(全局均是这个值) | 5/9(全局均是这个值) |
| 后验概率,发生某事件条件下属于这个类别的概率 | 3/5 | 2/5 |
2.3 示例3
某学校组织学生进行答题比赛,已知共有4道A类试题,8道B类试题,12道C类试题,学生从中任选1道该题作答,学生甲答对A,B,C这3类试题的概率分别是1/2,1/4,1/6,若甲答对所选试题,则这道题是B类试题的概率为【2023春 重庆-高二校联考期中】
解答
分类(事件)总和为4+8+12=24
分类(事件A)A类试题的概率是P(A类试题) = 1/6
分类(事件B)B类试题的概率是P(B类试题) = 1/3
分类(事件C)C类试题的概率是P(C类试题) = 1/2
分类(事件A)答A类试题条件下(或者理解:范围下)答对所选试题的概率,即条件概率P(答对 | A类试题)=1/2
分类(事件B)答A类试题条件下(或者理解:范围下)答对所选试题的概率,即条件概率P(答对 | B类试题)=1/4
分类(事件C)答A类试题条件下(或者理解:范围下)答对所选试题的概率,即条件概率P(答对 | C类试题)=1/6
同样的,对于全概率是没办法直接求出的,因此利用全概率公式
全概率公式
P(答对) = P(A类试题) × P(答对 | A类试题) + P(B类试题) × P(答对 | B类试题) + P(C类试题) × P(答对 | C类试题)= 1/4
直接使用贝叶斯公式
算“逆概率”即“答对所选试题,则这道题是B类试题的概率“
P( B类试题 | 凉答对) = P(B类试题) × P(答对 | B类试题) / P(答对)= (1/3) × (1/4) ÷ (1/4) = 1/3
3 对贝叶斯公式另外一种理解
其实还有一种对贝爷斯公式的理解和解法,即分类用乘法法分步用加分的概念
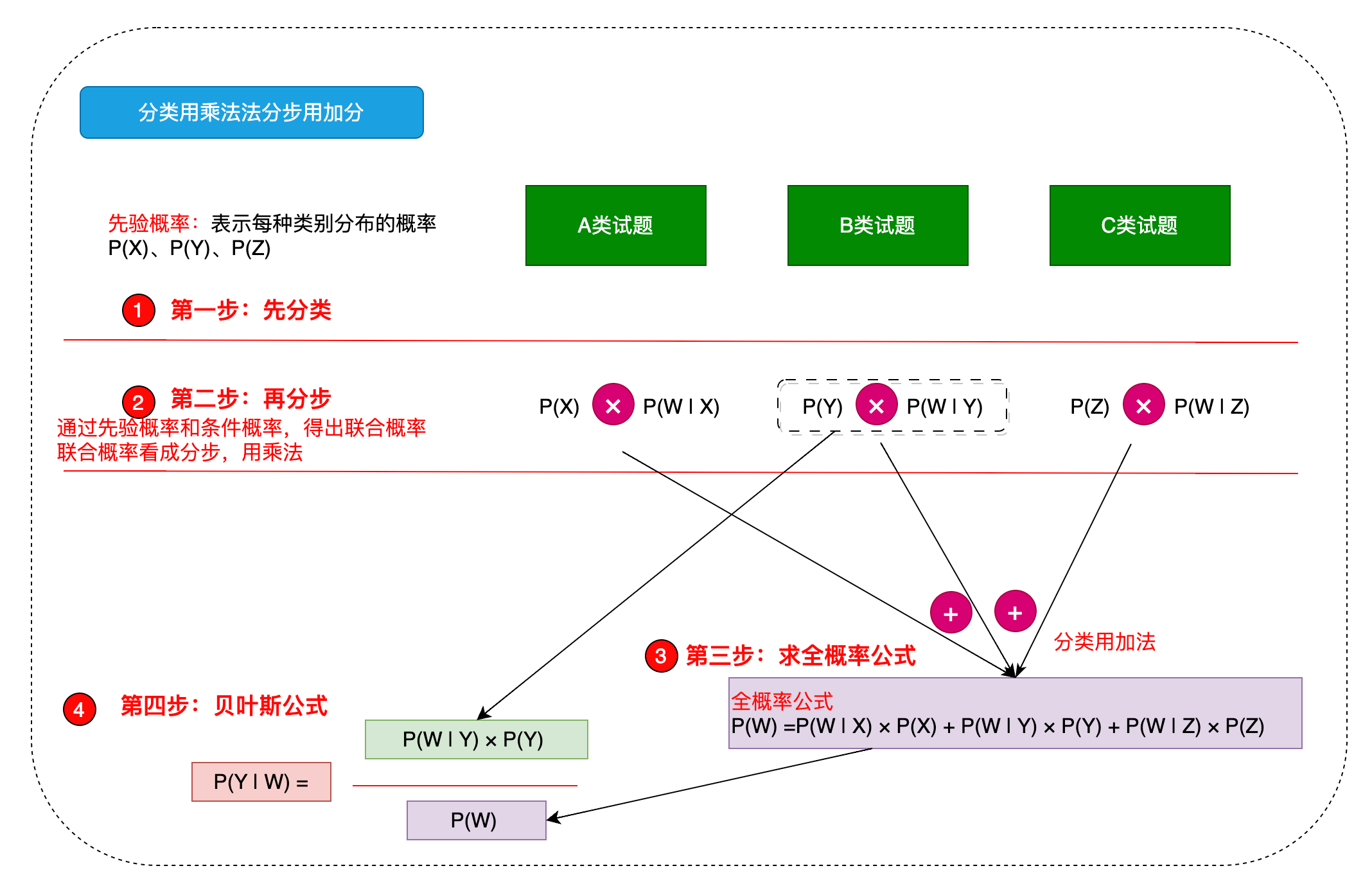
3.1 分类
就是把分类(事件)看成分类,例如:
示例1中的爷爷和奶奶
示例2中的男性和女性
示例3中的各类试题
简单理解就是先验概率P(X)
3.2 分步
分步可以看成在限定条件下,即在分类范围下的事件发生概率,例如:
示例1中,在爷爷或者奶奶的总红包数量范围下,抽中100元红包的概率
示例2中,在男性或者女性限定条件下,穿凉鞋的概率
示例3中,在回答各类试卷的范围,答对的概率
这里的概率就是条件概率,条件概率的分母只是在所在分类或者范围下,这个分类的汇总总和
条件概率形式上使用P(W | X)或者P(答对 | B类试题)或者P( 男性 | 凉鞋) ,中间为竖线
3.3 全概率
此时再通过分类用乘法法分步用加分的概念,就是先用分步的思想得出各事件在全局(包含各分类的视觉下)算出全局的概率,就是联合概率
联合概率就是表示两个事件共同发生的概率
计算出同时满足各分类下各事件发生的概率后,再通过分类相加的思想,得出的就是该事件在全局的全概率