数论之图解整除

最近做了几道AMC的排列组合和概率的数学题，发现数学的解题思维长期不用真的会逐渐腐朽

在过去的半年中我陆续学习点RNN和Transform等机器学习的理论知识，越发认识到数学作为基础科学的重要性，也曾经写过《一图三例说明白贝叶斯公式》的公众号文章

很多时候，我们都听到过数学之美的概念，历史上许多学者、数学家对数学美从不同的侧面作过生动的阐述

数学之美还在于其对生活的精确表述、对逻辑的完美演绎，可以说正是这种精确性才成就了现代社会的美好生活

数学在人工智能中起着至关重要的作用，它为人工智能提供了数学基础和工具，支持人工智能的算法和模型的设计与实现

神经网络的设计和训练涉及到数学中的线性代数、微积分和概率论等

数据分析涉及到统计学、概率论和数值方法等数学工具，用于解释数据、构建模型和进行预测

机器学习方法包括监督学习、无监督学习、强化学习等，这些方法背后都依赖于数学中的统计学、优化理论、线性代数等

万丈高楼平地，本系列文章希望能够以AMC American Mathematics Competition为基础，仍然参照《一图三例说明白贝叶斯公式》，以图解的方式去记录学习数论、排列组合，包括后续概率论、线性代理等一些知识点

以图解的方式去归纳总结知识点，相较于文本而言，对于人类大脑更加的方便记忆和学习复习

1 整除的定义

长期以来，谁被谁整除，谁是除数，谁是被除数，傻傻分不清楚

整除:当两个整数a和b(b!=0)，a被b除的余数为0时,商是整数,则称a能被b整除或b能整除a，这时称a是b的倍数,b是a的约数,并记作b | a

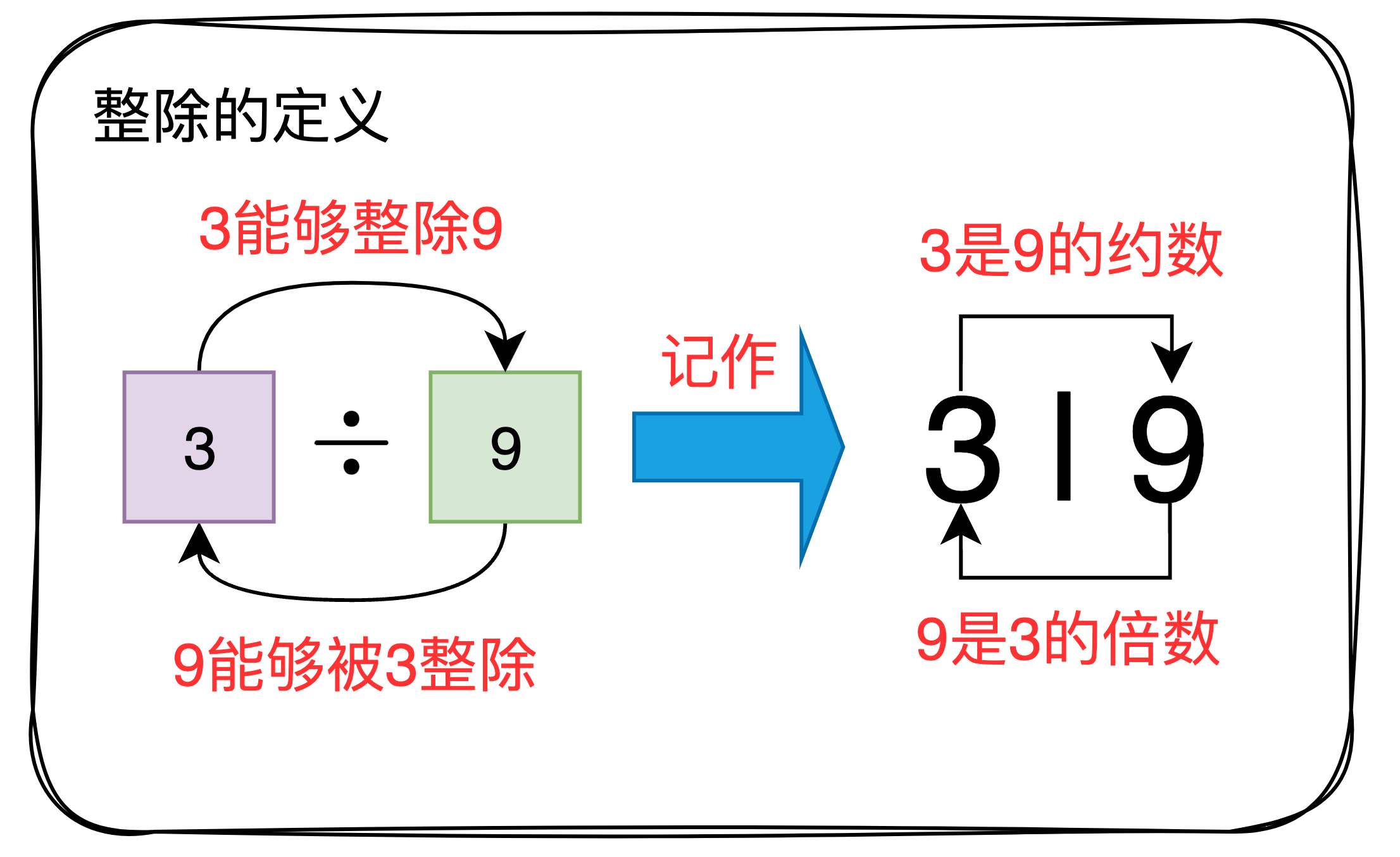
重要性：这里要记住约数的定义，即图解中3的定义

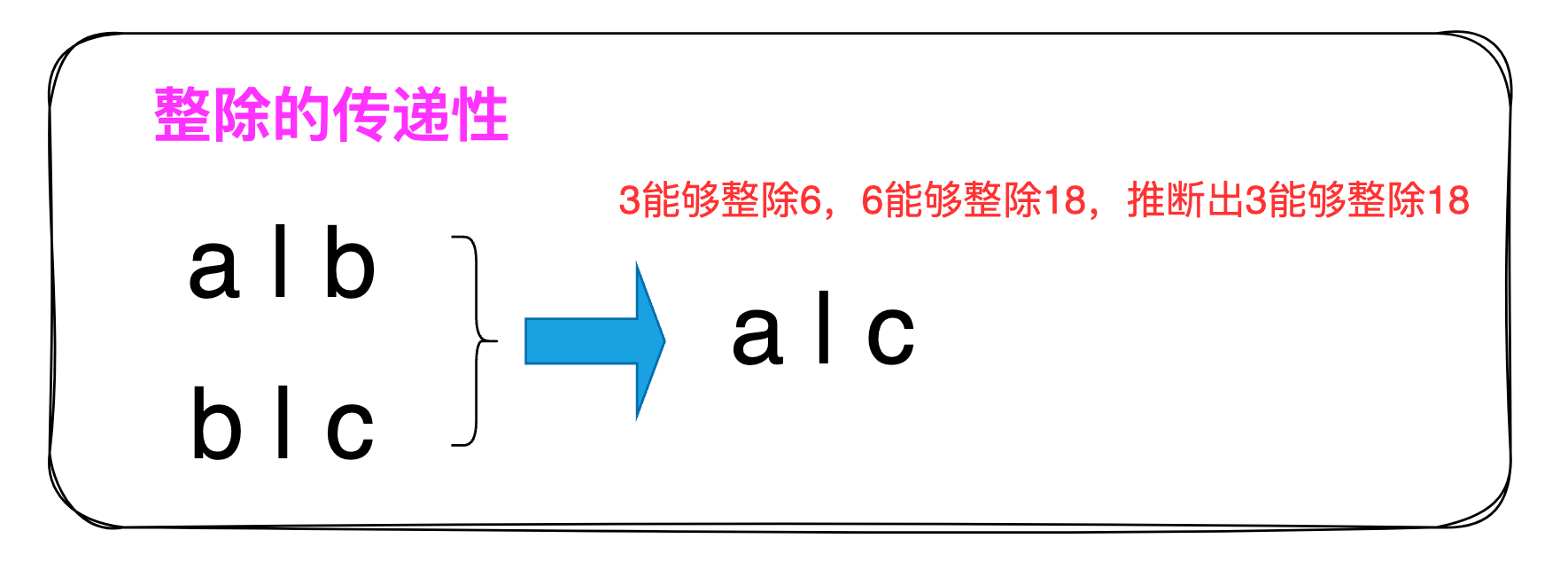
1.1 整除的传递性

若a|b且b|c则推断出a|c

得出另外一个重要定理：任何数的整除判定方式，都能传递给他的约数

所以一个数是否能被33整除，能够使用是否能被99整除这种方法

2 整除的判定

整除的判定总的来说分为尾系、和系、差系

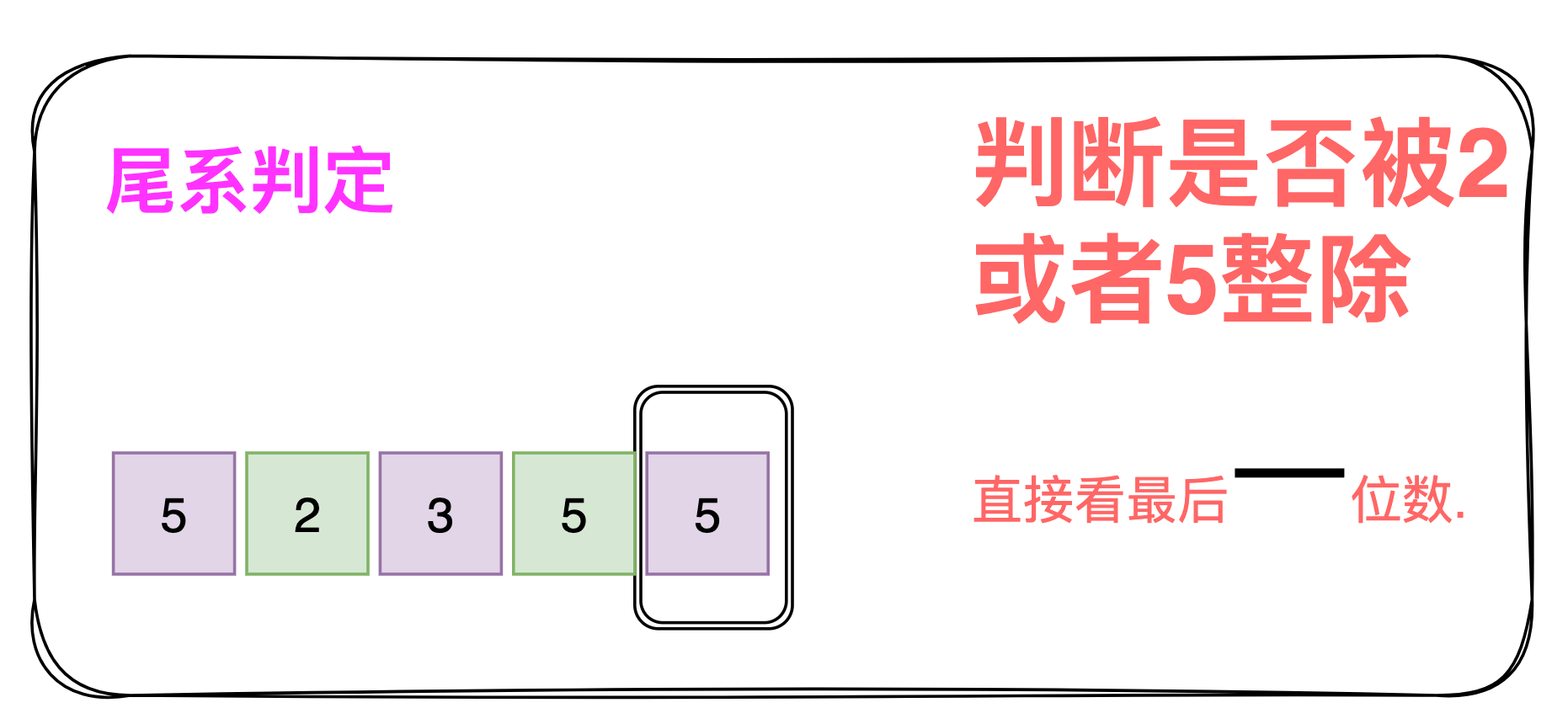
2.1 尾系判定

2和5：末位，即：一个数的末位能被2或者5整除，这个数就能被2或5整除

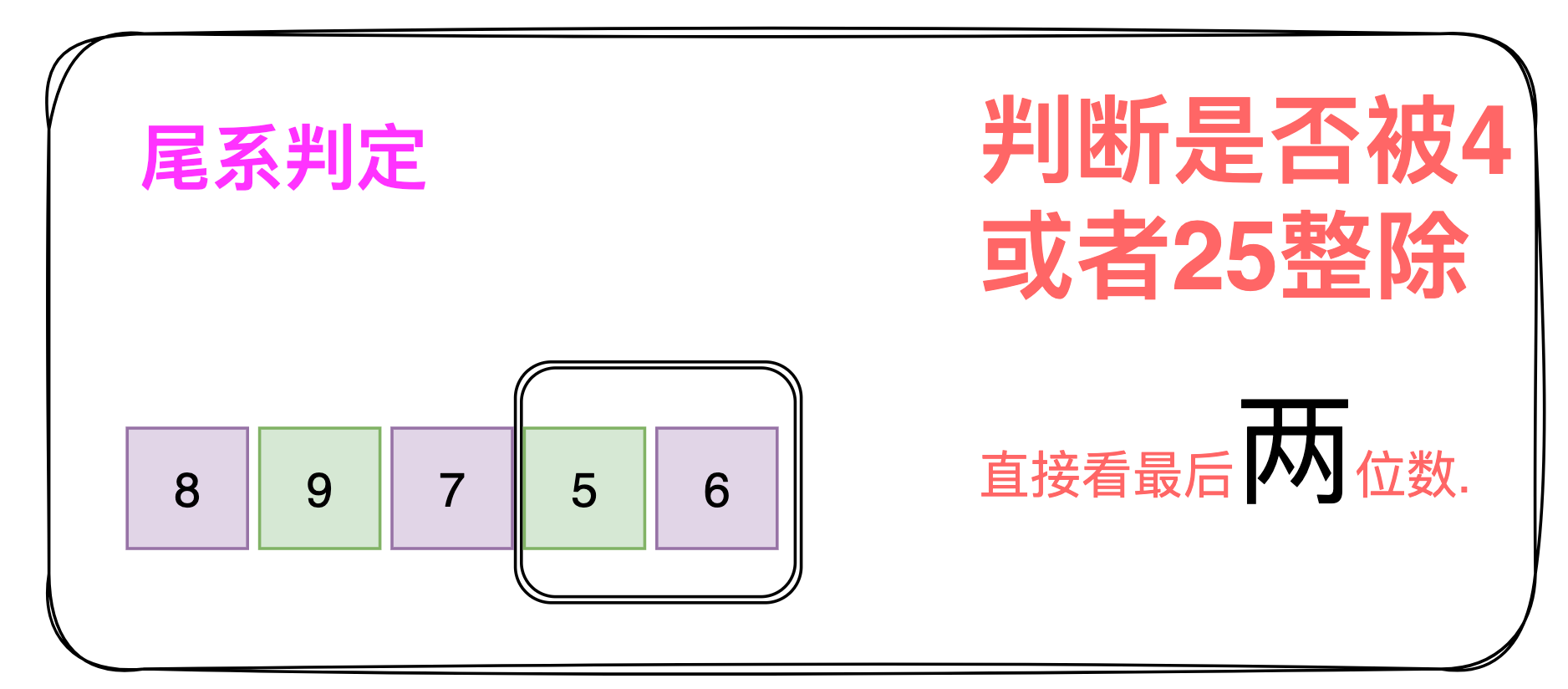
4和25：末两位，即：一个数的末两位组成的两位数能被4或者25整除，这个数就能被4或者25整除

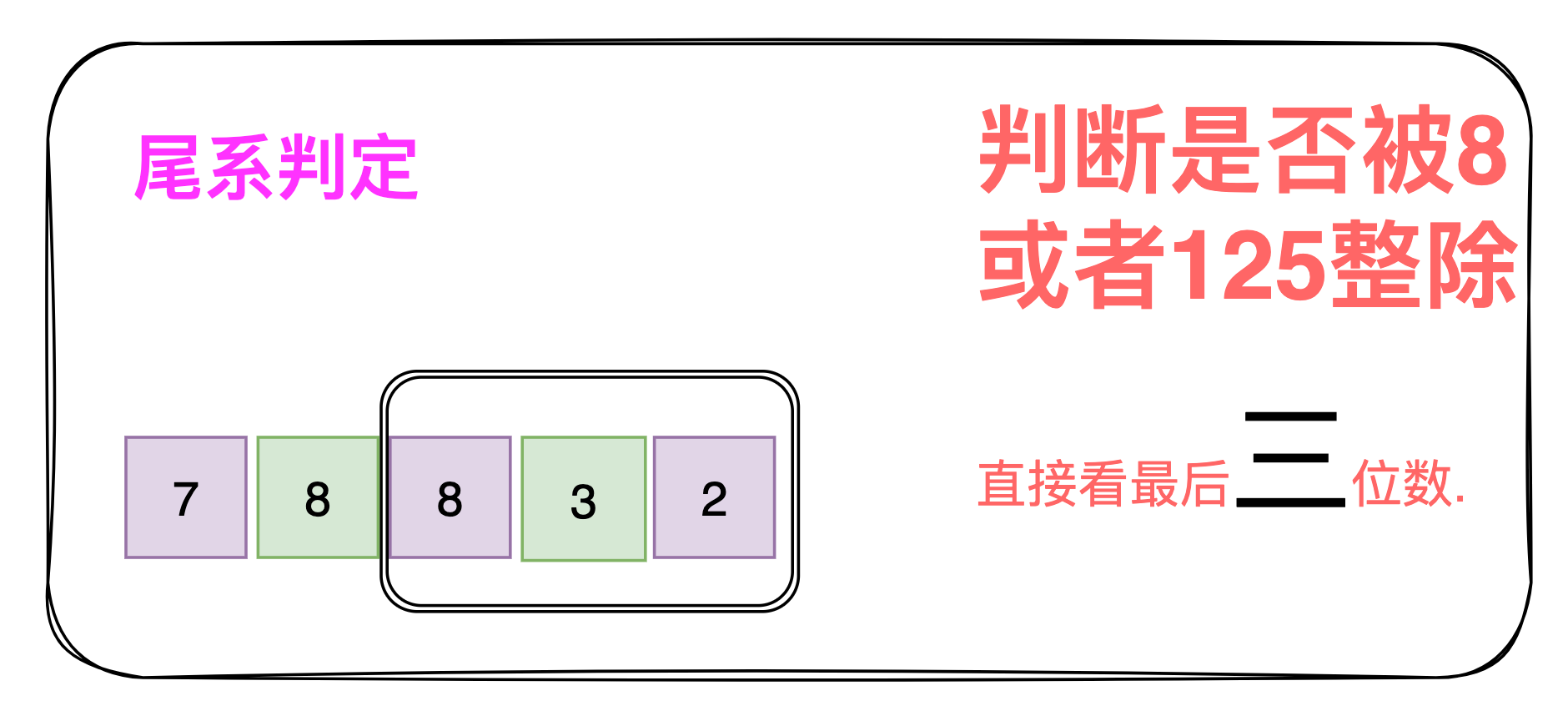
8和125：末三位，即：一个数的末三位组成的三位数能被8或者125整除，这个数就能被8或者125整除

2.2 和系判定

9和3：各位数字之和，即：一个数所有位数字和能被9或者3整除，这个数就能被9或者3整除

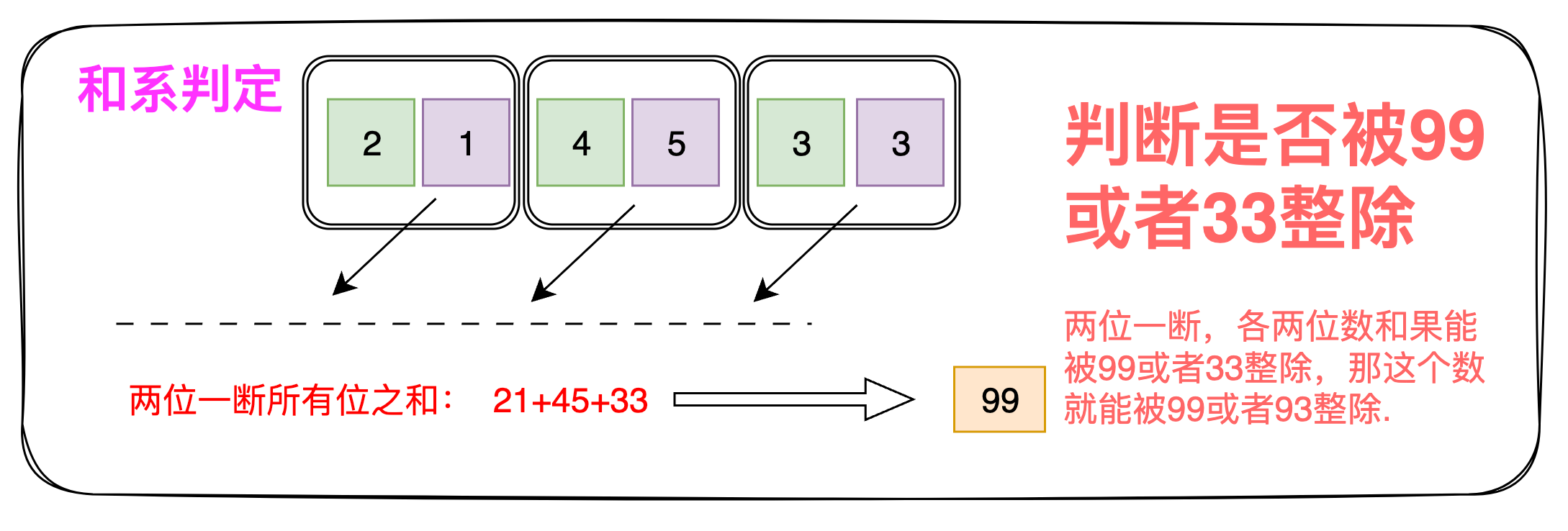
99和33：各位数字之和，即：两位一断求和，和能被99或者33整除，这个数就能被99或者33整除

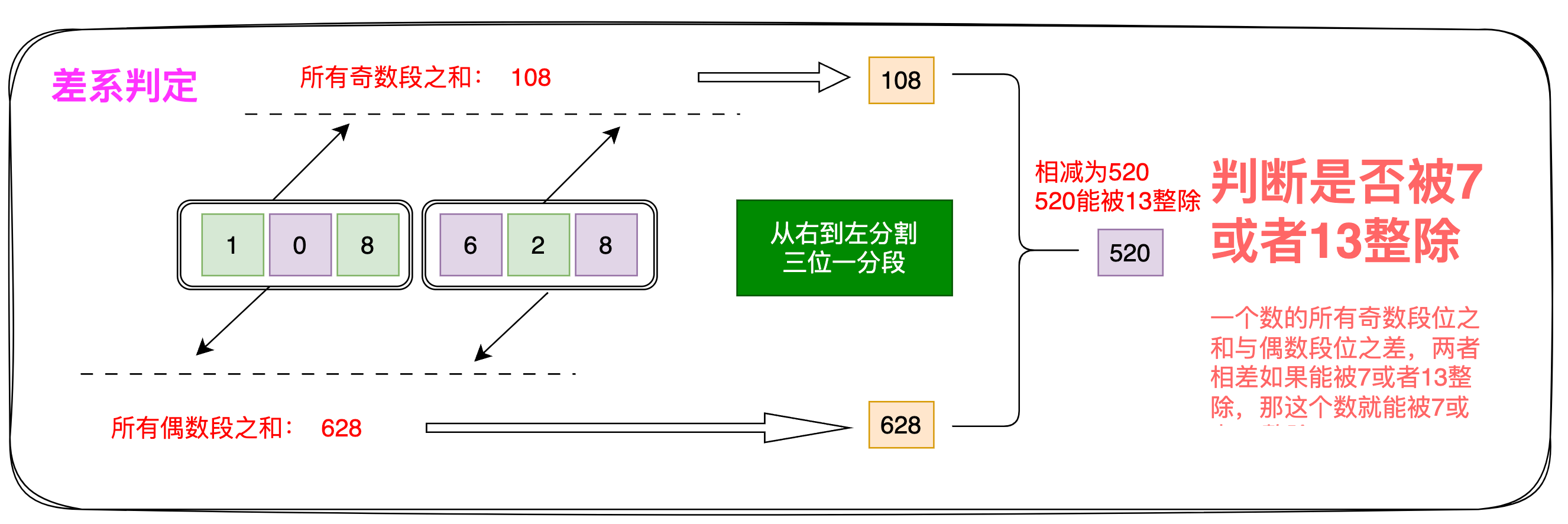
2.3 差系判定

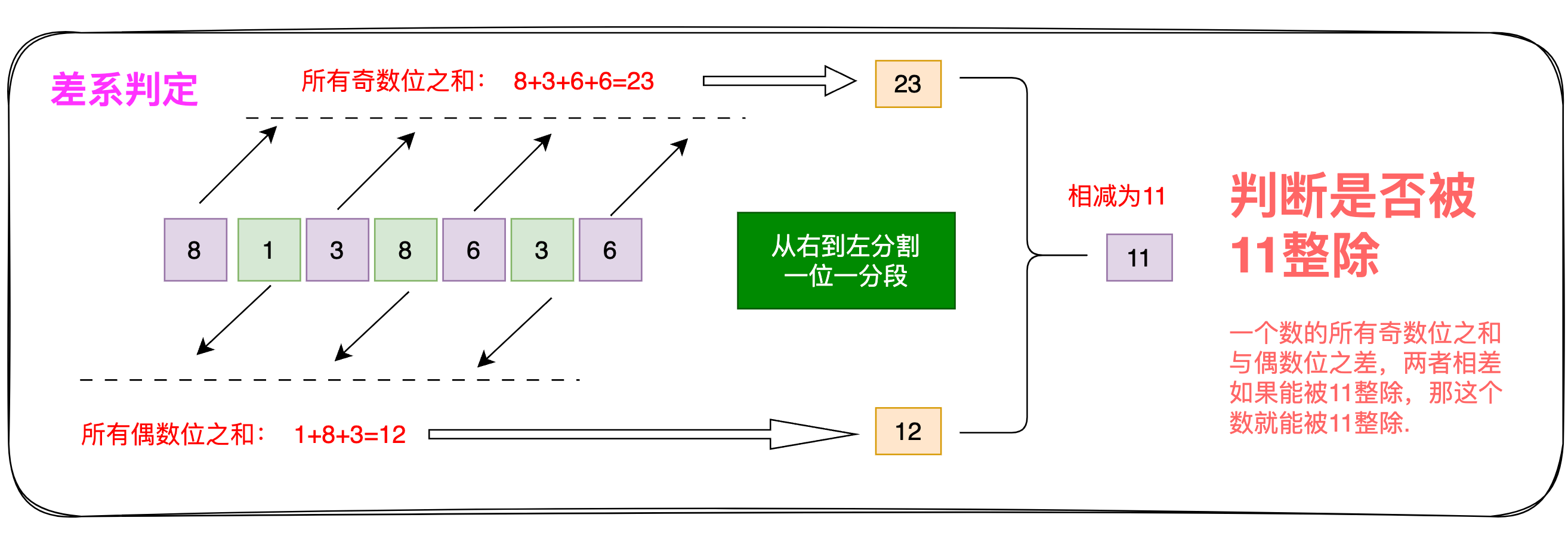
11：如果一个整数的奇位数（从右往左）上的数字之和与偶数位上的数字之和的差能被11整除，那么这个数能被11整除

101：两位一分段，如果一个整数的奇位数段（从右往左）上的数字之和与偶数段上的数字之和的差能被101整除，那么这个数能被101整除

注意是两位一分段，仍是从右到左分割

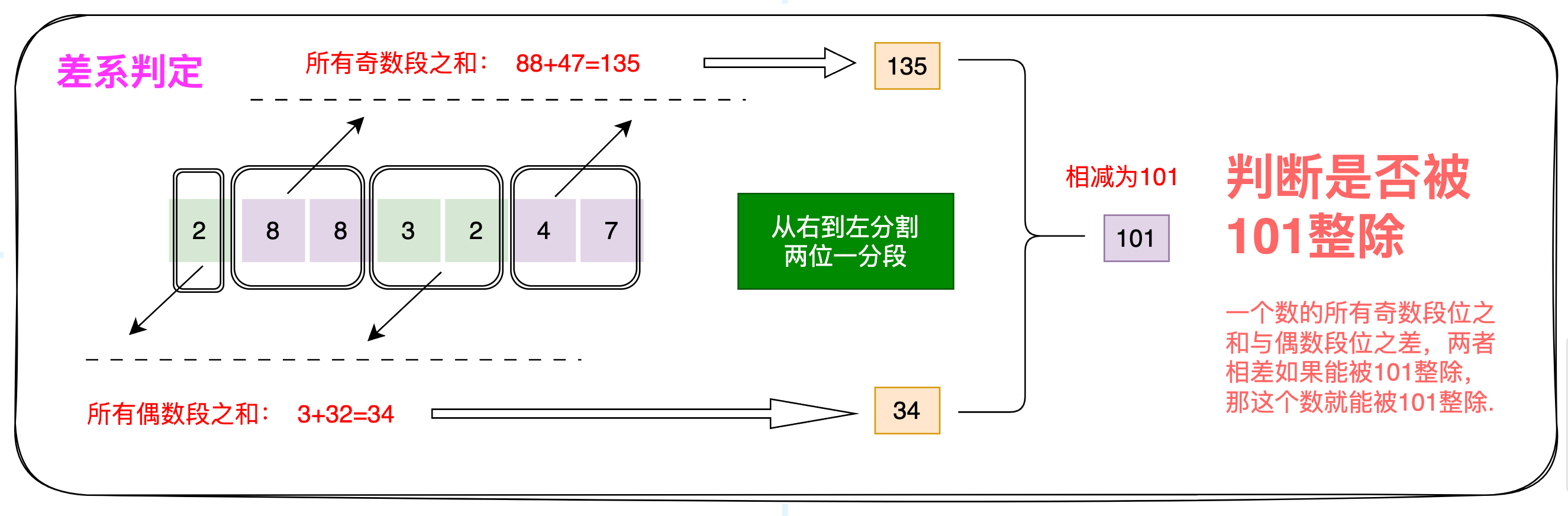
7、13：三位一分段，如果一个整数的奇位数段（从右往左）上的数字之和与偶数段上的数字之和的差能被7或者13整除，那么这个数能被7或者13整除

注意是三位一分段，仍是从右到左分割